Fast derivatives of likelihood functionals for ODE based models using adjoint-state method

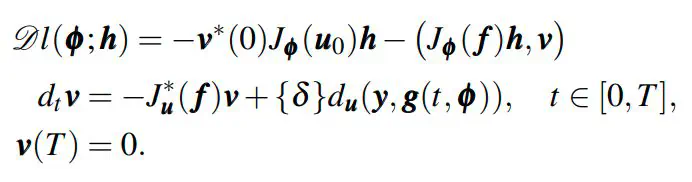
Abstract

We consider longitudinal data modeled by ordinary differential equations (ODEs), widespread models in physics, chemistry, biology and science in general. The sensitivity analysis of such dynamical systems usually requires calculation of various derivatives with respect to the model parameters. We employ the adjoint state method (ASM) for efficient computation of the first and the second derivatives of likelihood functionals constrained by ODEs. Essentially, the gradient can be computed with a cost (measured by model evaluations) that is independent of the number of the parameters and the Hessian with a linear cost in the number of the parameters instead of the quadratic one. The sensitivity analysis becomes feasible even if the parametric space is high-dimensional. In the theoretical part we rigorously study the ASM in the statistical context, when the discrete data are coupled with the continuous ODE model. Further, we present a highly optimized implementation of the results and its benchmarks on a number of problems.